 |
|
|
Hybrid SystemsThis version of the paper is for reading online. For a printed version please download the Postscript file to obtain best results. If you cannot see the equations online please read these notes. Approximation of Hybrid Systems by Neural NetworksAndrew D. Back1 and Tian-Ping Chen2
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(1) |
where we define the space of operators as existing on a compact set Ko,Fa Î Fa Í Ko, Fb Î Fb Í Ko.
For a definition of recurrent networks, see for example [14]. The hybrid model is a combination of nonlinear ordinary differential equations (ODEs) and discrete event dynamical systems (DEDs). A suitable definition of a hybrid system is given as follows [2].
Definition 2 A continuous output discrete time hybrid system is defined by
|
(2) | ||||||||||||||||||||||||
where x(t) Î Rn is the state, u(t) Î Rm is the control input, zëpû Î Z is the symbolic input, where Z is isomorphic to a subset of N+, y(t) Î Rp is the output, p(t) Î R, ëpû Î Z is a scalar given by the largest integer less than or equal to p, é p ù is the smallest integer greater than p, tp is the time t for which p last passed an integer value (i.e. the last time step of the symbolic dynamics), vëpû Î V Ì Z+ is a symbolic control input
a:Rn×Rm×Z® Rn, b:Rn×Rm×Z® R, g:Rn×Z×V® Z, and z:Rn×Z® Rp.
We shall state some pertinent theoretical results below. Due to space constraints, proofs will be omitted.
2.2 Constructive Existence Result
The existence of a physical model which can implement an operational map is given by the following lemma.
Lemma 1 A model G with continuous, real-valued input input and outputs x(t) Î X Í C( K) , y(t) Î Y Í C( K) , respectively, consisting of the interconnection of a parameterized operator F(q):C(K) ® C( K) , and functional Mc:C( K) ® Rm according to
|
(3) | ||||||||||||||
where t Î R+, and q(x) is the m-dimensional parameter vector of F is capable of implementing a general operational map H(q):Fa® Fa, where Fa Î Fa Í Ko and Fb Î Fb Í Ko.
2.3 Universal Approximation of Operational Maps
If a model can approximate any operational map arbitrarily well, then it can approximate any multiple model arbitrarily well. Such a property may be defined as universal approximation of an operational map. We give some of the main theoretical results below without proof.
Theorem 1 There exists a parameterized model G(q):x(t),[^y](t-1)® [^y](t), and a system H:x(t),y(t-1)® y(t) such that
|
(4) |
where where x Î X Í C( K) , [^y] Î [^Y] Í C( K) , y Î Y Í C(K) , e > 0 and T is some finite time.
Theorem 2 There exists a parameterized model G([^(q)]):x(t),[^y](t-1)® [^y](t) given by the interconnection of a universal operator F(q):X×[^Y]×V® [^Y] and a single-input single-output universal functional Mv:X×[^Y]® V according to
|
(5) | ||||||||||||||||||||||||||||||
where x Î X Í C( K) , v Î V Í C( K) , [^y] Î [^Y] Í C(K) , [^(q)] Î [^(Q)] Í Rmand a system H:x(t),y(t-1)® y(t) which implements an operational map such that
|
(6) |
where y Î Y Í C( K) , e > 0 and T is some finite time.
Hence, these results indicate that the universal approximation result for recurrent networks [14] are applicable, and therefore, there exists a constant recurrent network which is capable of approximating multiple systems Si i = 1,2,...,m. Moreover, it is clear that such approximations may be made individually to an arbitrary degree of accuracy. This follows from consideration of the increased dimensions of approximation space of the network. These theorems give a mechanism by which multiple modelling can take place in neural networks
3 Hybrid Systems and Neural Networks
3.1 Architectures
The results given in section 2 indicate that novel modular neural network architectures can be used to construct operational maps. This leads us to obtain the following results concerning the relationship between hybrid systems and operational maps, and hence neural networks and hybrid1 systems. From (5) and Theorem 2.2 we obtain the following result.
Theorem 3 A hybrid system is an operational map.
Theorem 4 There exists a parameterized model G([^(q)]):x(t)® [^y](t) given by the interconnection of a universal operator F(q):X×V® [^Y] and a single-input single-output universal functional Mv:X® V according to
|
(7) | ||||||||||||||||||||||
where x Î X Í C( K) , v Î V Í C( K) , u Î U Í C( K) or u Î U Í R, [^y] Î [^Y] Í C( K) , [^(q)] Î [^(Q)] Í Rmand a system H:x(t)® y(t) which implements an operational map such that
|
(8) |
where y Î Y Í C( K) is the output of a hybrid model [`({ a,b,g,z} )] , with [`({ a,z} )]:x(t)® y(t) and e > 0.
Corollary 1 A hybrid model can be approximated by a recurrent neural network.
The implication of these results, is that it is possible for a neural network to approximate a hybrid system with arbitrary accuracy. This result shows that it is possible to treat hybrid models from a neural network perspective. Intuitively, one may have suspected this to be the case, since it is known that recurrent neural networks can approximate finite state automata2 [4], a commonly used component in hybrid systems, and in general, they can approximate the solutions of various ODEs. The results in this paper make it clear that recurrent networks possess very general, universal approximation capabilities for hybrid systems. The results given here can also be interpreted in terms of Sontag's PL map framework [15] which we do not go into here due to lack of space.
4 Synthesis of Neural Network Hybrid Models
In this section, we give some practical aspects and examples of synthesizing hybrid models based on neural network structures.
There are numerous methods in which models can be derived based on the framework presented in this paper. Here we shall only attempt to give a brief summary of some of those methods and examples of each. Clearly this will not be exhaustive, but representative of some techniques only.
4.1 M{c,v} Subsection
The M{c,v} model subsection implements the discrete state dynamics. For convenience, we will refer to this subsection as Mc. The basic idea is that Mc implements the symbolic level processing in a neural network structure. For example, this may be a decision tree, a DFA [4], or some more complex computational device [13].
For convenience, it is useful to break Mc into three further modules: Mc1, Mc2 and Mc3. Depending on the quantization or classification performed by Mc1, the symbolic processing in Mc2, and the decoding performed in Mc3, F will switch between different models.
4.2 F Subsection
The F model subsection is a real-valued continuous state model. One of the simplest examples is the linear filter given by
|
(9) |
Clearly, F can also be implemented as a more complex nonlinear operator. Using q = Mcx(t) allows Mc to switch the base model F into a number of discrete states. As indicated by Theorems 3 and 5, another approach is to use Mc to drive the input of F giving a similar result. These methods are termed the parameter replacement and augmented input form of coupling Mc and F.
4.3 Augmented Input Networks: Hybrid Models by Bias Shifting
Here we present a simple constructive approach to show how multiple models may be synthesized in both feedforward and recurrent neural networks. The approach we propose is well suited for multiple models which are comprised of a set of discrete F models.
The fundamental approximation capabilities of neural network models come about due to the ability to sum basis functions comprised of sigmoids, which are local in the input space. That is, the flatness of the sigmoids' tail implies that we can add as many sigmoids as required to form an approximation and the effect can be made local. Accordingly, we may deduce the following constructive method.
An RNN model G(x,y,v) can form multiple unique function mappings
|
(10) |
defined by
|
(11) |
where the extra input v indexes the desired mapping mv(x,y).
The implication of this is that by appropriate biases offsets in the different groups of units, it is possible to obtain universal approximators in each subgroup of units over a finite range. This finite range is not a problem however, since we can always make r arbitrarily large in order to keep the individual mappings separated. Each of the subgroups may define unique mappings, activated by the appropriate input v.
We term this constructive method of synthesizing multiple models bias shifting. This method can be used as a means of switching between different models.
5 Examples
5.1 Bias-shifted MLP
As a simple example of the bias shifting method, consider a multiple model feedforward network3. The network is a two-weight layer network in which there are two groups of hidden units. The mappings pertaining to each group of weights are obtained simply by providing different inputs to the network are shown in Fig. 1. In other words, the network `contains' two quite different function approximations. According to the value of the input signal, it is possible to select which of the two mappings will be used.
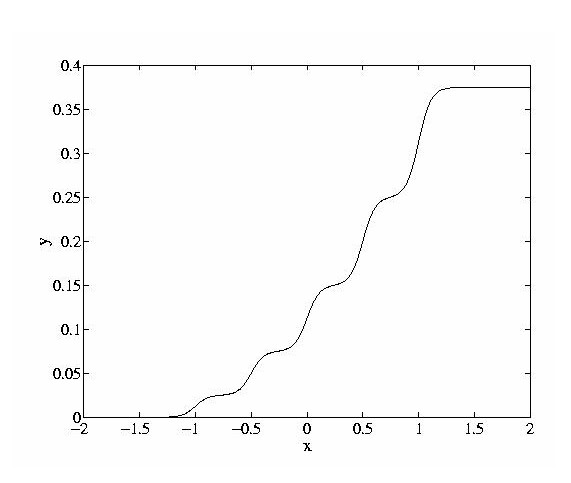
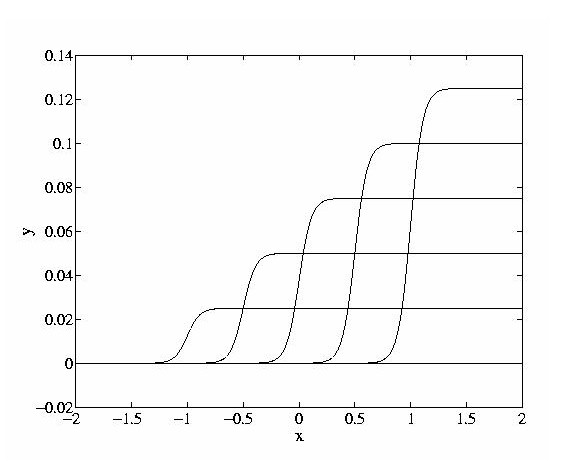
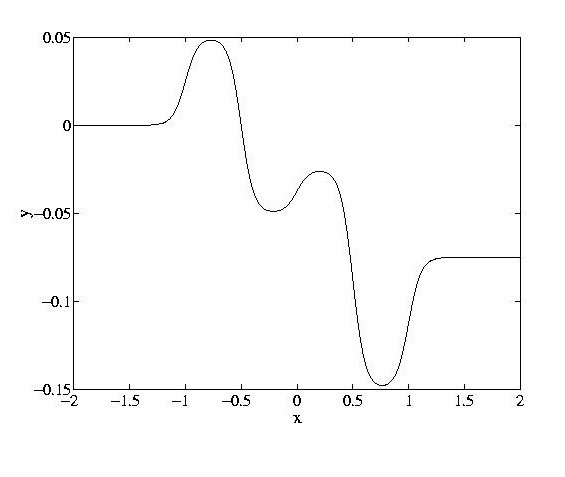
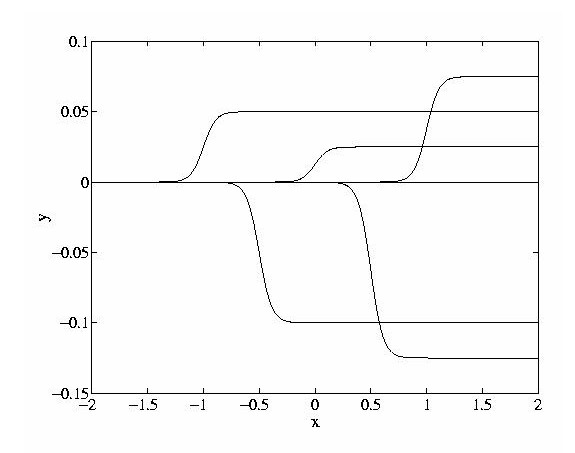
Figure 1: An example showing the use of bias-shifting to select different function
approximations. The input-output mapping and hiddent unit outputs are shown for each case.
Note that these mappings coexist within the one network, but one is ``selected'' for the
inputs at any given time, due to the function Mc, which outputs the extra input
bias v.
5.2 A Recurrent Network Hybrid Model
In this example, we propose a hybrid model based on the recurrent network. An interesting aspect of this model is that it is structurally similar to the usual pole-zero linear model, but the actual pole-zero positions are determined by nonlinear functions. The model is described as follows.
|
(12) | ||||||||||||||||||||||
where { M{c,d}i} are the element-wise characteristic functions of the vector function equation q = Mc(u), corresponding to the previously developed notation. Since the poles and zeros in (19) are the outputs of nonlinear functions, they are termed nonlinear poles and zeros respectively and the model can also be considered as a nonlinear pole-zero model.
The coefficient functions { Mc} and ancillary inputs{ u} provide a wide scope for introducing a variety of models. For example, Mc may be the discrete state automata as indicated earlier, implementing some linear or nonlinear function of time t, inputs { x} , and outputs { y}. Indeed, other auxiliary variables can also be naturally introduced at this point.
If M{c,d}i( ui) = qi, then a linear model will result. However, by the appropriate choice of { M{c,d}i} , (19) is capable of representing a range of time-varying linear models. Moreover, such models can generalize existing structures in an intelligent manner. Similar models have been recently considered in the literature [8]. It is interesting to note however, that while this model conforms to the general hybrid system framework, it can be viewed as an RNN with nonlinear synapses.
6 Conclusions
In this paper, we have given a new framework for understanding dynamic neural network models. Operational maps define mappings from one operator space to another operator space. Theorems showing the existence of neural network universal operational map approximations have been given. The framework of operational maps has been used to prove that a general class of hybrid models can be approximated arbitrarily closely by a recurrent neural network. We have given an indication of how such models may be synthesized. While we have not considered it in this paper, it would be interesting to devise a method, if one exists, which would allow the extraction of the subsystems described in this paper from a trained RNN structure. If this can be done, it may provide some useful insights into the function of trained recurrent networks, particularly in terms of nonlinear system identification models.
References
- [1]
- M. S. Branicky, V. S. Borkar, and S. K. Mitter. A unified framework for hybrid control: background, model, and theory. Technical Report LIDS-P-2239, Laboratory for Information and Decision Systems, Dept of Electrical Engineering and Computer Science, MIT, June 1994.
- [2]
- R. Brockett. Hybrid models for motion control systems. In Perspectives in Control, pages 29-54, Boston: Birkhauser, 1993.
- [3]
- L.A. Feldkamp, G.V. Puskorius, and P.C. Moore. Adaptation from fixed weight dynamic networks. In Proceedings of IEEE International Conference on Neural Networks, Washington (ICNN '96), pages 155-160, 1996.
- [4]
- C.L. Giles, C.B. Miller, D. Chen, H.H. Chen, G.Z. Sun, and Y.C. Lee. Learning and extracting finite state automata with second-order recurrent neural networks. Neural Computation, 4(3):393-405, 1992.
- [5]
- R. A. Jacobs, M. I. Jordan, S. J. Nowlan, and G. E. Hinton. Adaptive mixtures of local experts. Neural Computation, 3(1):79-87, 1991.
- [6]
- D. Lainiotis. Partitioning: A unifying framework for adaptive systems I. estimation. Proc. IEEE, 64:1126-1143, 1976.
- [7]
- D. Lainiotis. Partitioning: A unifying framework for adaptive systems II. control. Proc. IEEE, 64:1182-1197, 1976.
- [8]
- K. Narendra, J. Balakrishnan, and M. Ciliz. Adaptation and learning using multiple models switching and tuning. IEEE Control Systems Magazine, 15(3):37-51, 1995.
- [9]
- Anil Nerode and Wolf Kohn. Multiple agent hybrid control architecture. Technical Report TR 93-12, Mathematical Sciences Institute, Cornell University, Ithaca, New York 14850, March 1993.
- [10]
- E. Ronco and P.J. Gawthrop. Modular neural networks: a state of the art. Technical Report CSC-95026, Center for System and Control, University of Glasgow, May 1995.
- [11]
- I.W. Sandberg. Approximation theorems for discrete-time systems. IEEE Trans. Circuits, Syst., 38(5):564-566, 1991.
- [12]
- J. Schmidhuber. Learning to control fast-weight memories: An alternative to dynamic recurrent networks. Neural Computation, 4(1):131-139, 1992.
- [13]
- H. T. Siegelmann and E. D. Sontag. Turing computability with neural nets. Applied Mathematics Letters, 4(6):77-80, 1991.
- [14]
- E. Sontag. Neural nets as systems models and controllers. In Proc. Seventh Yale Workshop on Adaptive and Learning Systems, pages 73-79. Yale University, 1992.
- [15]
- E.D. Sontag. Interconnected automata and linear systems: A theoretical framework in discrete-time. In R. Alur, T. Henzinger, and E.D. Sontag, editors, Hybrid Systems III: Verification and Control, pages 436-448, NY, 1996. Springer, Birkhäuser Verlag, Basel.
Footnotes:
1 Due to the many different definitions for hybrid systems, we do not seek to prove the results for all known classes of hybrid systems, but rather we have chosen to show the results for one relatively general model. From these results it is straightforward to extend the results to other classes of hybrid systems [1].
2 Note that a recurrent network implementing a finite automata can be used in place of the submodel Mv, however more general models are clearly possible.
3 As a means of demonstrating the technique, we use a feedforward network only.
File translated from TEX by TTH, version 1.57 with some help by Andrew Back.
|
|
| Home
|
|
|
|
Copyright © 1989-2008 Andrew Back. All Rights Reserved. |